Torque causes rotation. It is equal to force multiplied by lever arm [torque=force X lever arm]. The farther the lever arm is from the axis of rotation, the less force is required for an object to rotate. A paddle is required in order to kayak. One of the key points of this paddle, is how you hold it. The farther apart you place your arms, the easier it will be to paddle because the lever arm will be increased and the force required to move the paddle will be much less than if you were to hold the paddle with your arms close together. Although your rotational inertia would decrease because you would be holding the paddle closer towards its axis of rotation, the lever arm would be decreased therefore the force required to move the kayak would increase.
This
unit was particularly interesting because the physics we learned seemed to
relate to ever day activities even more than before.There are three main topics we learned about this unit;
rotational and tangential velocity, rotational inertia, the conservation of
angular momentum, torque, center of mass/gravity, and centripetal and
centrifugal forces.
Rotational
velocity is the number of complete rotations per time unit. Tangential velocity
can also be called linear speed because it is something moving a long a
circular path. The direction of motion is tangent to the circumference.
Tangential speed depends on the distance from the axis of rotation. Take a
merry-go round for instance, the closer you are to the middle the slower you
are going whereas on the outside you feel as though you are going much faster.
This is because the people on the outside are farther from the axis of
rotation. Everyone has the same rotational speed. Their rotational speed is
dependant upon the number of spins the platform of the merry-go round has per
time unit.
Another example is a track race. If
everyone started in an exact straight line, the race would be unfair because
the people on the outside would have to have a greater speed to keep up with
the people closer to the axis of rotation who would not need to go as fast. The
runners on the outside would have a greater tangential velocity than the
runners on the inside. Each runner has his or her own rotational speed
depending on the speed in which they are going.
Have you ever seen a car with tires
much too big for its frame? Well these people most likely get speeding tickets
frequently if they are not careful. A speedometer is accustomed to a specific
size of tires, therefore when you get larger tires than the speedometer is
accustomed to the car might read 40mph but you are really going 60mph. Although
your rotational speed decreases, your tangential speed increases and you are
covering a greater distance in a smaller amount of time because your wheels are
larger.
The last example we learned a lot
about is the wheels of a train. The wheels are designed with the wider parts in
the middle rather than the outside. The wider parts are in the middle because
the wider parts will allow the wheels to turn and go straight. The smaller
parts of the wheel will want to turn and the larger parts will direct the
wheels to remain on the tracks. In this scenario the left diameter on the track
is smaller than the right therefore it will move slower and the right will move
faster causing the wheel to curve inward. If it shifts too far where the larger
diameter is on the left, it will move faster causing the train to curve in the
opposite way, it is a method of self-correction.
Moving on to rotational inertia;
Inertia is the property of an object to resist change in motion dependant upon
the mass. Rotational inertia is the property of an object to resist changes in
the spin of an object. It is dependant upon, not the mass of each object, but
where the mass is located on that object, how it is distributed. It involves the distribution of mass and
how far away it is from the axis of rotation. If an object has a small amount
of rotational inertia, it is easier to spin compared to an object with a large
amount of rotational inertia, which is very difficult to spin.
Rotational inertia explains why
runners bend their legs instead of keeping them straight. By bending their
legs, their mass is closer to the axis of rotation lowering the rotational
inertia.
This can also explain how an ice
skater spins. When the ice skater has their leg and arms spread out and
spinning, their rotational inertia is much greater because her limbs are
farther away from his/her axis of rotation, therefore the ice skater is
spinning very slowly. However, if an ice skater brings in his/her arms and
legs, her rotational inertia decreases because she is bringing her mass closer
to her axis of rotation.
The conservation of angular and
rotational momentum is basically the same concept as the conservation of
momentum. Angular momentum is made up of two key factors: rotational inertia
and rotational velocity.Angular
momentum before equals the angular momentum just as the total momentum before
equals the total momentum after.
Conservation of Angular Momentum:
Rotational inertia X Rotational
Velocity (before) = Rotational inertia X Rotational Velocity (after)
Here’s an example of the ice skater
with angular momentum;
RI X rv (before) = ri X RV (after)
In this example, the ice skater started out with a large
rotational inertia (because she had her mass far from her axis of rotation)
therefore she had a small rotational velocity. Then, she had a small rotational
inertia (because she brought in her mass closer to her axis of rotation) and
had a large rotational velocity. We know this is true because of the conservation
of angular momentum, which informs us that the momentum before will always end
up equaling the momentum after.
Torque
is what causes an object to rotate. It equals the force of an object multiplied
by its lever arm (which is the distance from an object of rotation). If an
object has a large torque, it will have a large torque.A torque is the rotational counterpart
of force. Force changes the motion of objects whereas torque changes the
rotation. Just like rotational inertia, torque involves the distance from the
axis of rotation. This distance with torque is known as the lever arm.
In
this example, the ball on the left is hollow, therefore it a smaller force than
the ball on the right who has a larger force and although the both the ball on
the left side of the seesaw and the ball on the right side of the seesaw have
equal lever arms, the ball on the right has a greater torque because it has a
larger force therefore it has a larger torque.
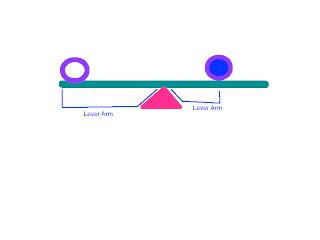However,
in this image notice that the lever arm on the left is larger than the lever on
the right. Therefore, the small force and large lever arm on the left balance
out the large force and small lever arm on the right. The lever arm on the left
was increased by simply having a greater distance from the axis of rotation.
This
is also common when dealing with bolts and wrenches. If there is a tight bolt,
you would want to have a wrench with a large lever arm because by just creating
a greater distance from the axis of rotation the force required to turn the
object will decrease and the amount of torque will be greater.
The
center of gravity is a term commonly used to express the center of mass. The
center of gravity is the average position of weight distribution. Center of
mass and center of gravity refer to the same point of an object. The center of
gravity must be above the base of support. When the center of gravity is
outside the base of support a torque happens. The center of gravity lies
directly beneath the point of suspension. The center of mass of an object may
be a point where no mass exist.
An
example where we see the center of gravity is the Leaning Tower of Pisa which
has the center of gravity lying above its base of the support therefore the
tower does no fall over. An object with a wide base and a lower center of
gravity is more stable.
A
centripetal force is a center seeking force. A centrifugal force is a center
fleeing force, however, it is a fictitious force. Think about a car going
around a turn. The friction between the tires and the road provides the
centripetal force that holds the car in a curved path. However if the friction
is not great enough, the car will skid off the road.
However,
inside this rotational system there seems to be an outward force. This outward
force is the centrifugal force. An example that might be able to explain this
more easily would be if you were a passenger of the car that was rounding the
turn. The car is turning left and you move outward to the right, technically
this was not because of a centrifugal force, it was because there wasn’t a centripetal
force to keep you in a circular motion.
This
unit was surprisingly difficult for me. The concept I struggled with the most
was torque. I was confused by the difference between torque and rotational
inertia. However, after going into conference period, I realized I needed to re
watch the torque video. In doing this, I mastered the concept and I examples in
the book involving torque.
My
problem skills throughout this unit progressively increased. At first, I
struggled with going into depth with each of the concepts presented to us. I
didn’t realize that I wasn’t going into enough depth until I began struggling
with torque. I realized I needed to be able to relate each of these concepts to
one another. So, I reviewed my notes from the previous videos and tried to find
any gaps I didn’t understand. To clarify my confusion on specific example, I
discovered that the book is actually really helpful. I think that was my key
discovery in my problem solving skills this unit (the book). My homework effort
this unit was very high and I didn’t miss an assignment and each assignment I completed
I didn’t think was just busy work, it was helpful when looking back and
studying it. Although I had a high effort in homework this unit, I need to work
on my participation in class. I am always focused in class, yet I don’t raise
my hand enough to ask questions or to answer questions. I think this could
really help me with clarifying concepts for me.
Our
podcast was a little frustrating because our group had a hard time coming up
with what to say, however, the product ended up as a really great study tool.
My original plan for solving this challenge problem worked,
however, it was much more complicated than it needed to be. We decided we would
just come up with a plan along the way. Naeem and I constructed a seesaw
instead of a countertop like the rest of the class. We rested the meter stick
on a book with the weight on one end and balanced the stick so that it appeared
horizontal. When doing this it was apparent that the side with the weight on it
had a larger lever arm than the side with the other weight. This is when we
took the formulas about torque and put them to use. The original formulas used:
t=t
t=force X leverarm
force X leverarm= force X leverarm
w=mg
clockwise torque= counter clockwise torque
After taking measurements we knew that the meter stick was
100cm. The side with the weight had a lever arm of 28cm and the side with the
meter stick balanced on it had a lever arm of 22cm. We also knew that the side
with weight had a force of 98. This is because the force on it was the force of
gravity and converting that to Newton’s it would be 98.
28
X 98= 22 X F
2744=22F
F=124.727N
The force of this really wasn’t far off yet this process
became a lot more complicated than it needed to be when the see-saw was made.
So, we followed the common method used by the class even though we got similar
answers either way. In the correct process we balanced the stick and the mass
off a tabletop. It took out the variable of the extra meter stick and we also
got different numbers. However the lever arms ended up in the same proportion
(the side with the weight had a larger lever arm than the other side). Another
thing that changed in this were the decimal points. We realized that last time
we had moved the decimal points of the force of gravity had been moved to the right
instead of the right so it actually should have been .98 rather than 98.
You don't need to watch the whole video if you have a full understanding of the basics behind torque. This source really helped me with a better understand behind torque. I liked the examples used to explain it. Although we went over the wrench example in class, it helped to have other examples with similar explanations too.
After completing homework assignments, lessons from class, and watching this video, this is my understanding of torque; Similar to a force, which is a push or pull, torque is almost as simple, it is a twist to an object. Speaking mathematically, torque is forceX the lever arm. Torque is mainly effected by these two factors (the force and the lever arm).
You can stop watching at about 1:50.
In this track race, everyone started at different distances. The people who start on the outside, are placed further ahead because they are farther from the center, therefore, they would be at a disadvantage if they started in a straight horizontal line at the start, the people would need to move faster than those people closer to the inner part of the track. The tangential speed is the distance covered per line. This is also known as linear speed. If the racers were to all start in the same line, the runner on the outside would have a faster tangential speed than the racers on the inner part of the track. The rotational speed also plays a key factor in races. Rotational speed is speed measured depending on the number of rotations per time. Therefore, the racers RPM depends on their personal speed not on their distance.
The fundamentals of running comes from physics too. All runners bend their legs when they run because they are moving their legs closer to their axis of rotation (their hips). We know this is important from the property of rotational inertia. Rotational inertia is the property of an object to resist changes in spin or rotation. It is not based upon the mass of an object, rather where that mass is located or how it is distributed (how far it is from the axis of rotation). Therefore, runners bring their mass closer to the axis of rotation to lower their rotational inertia. The farther away from the axis of rotation, the higher rotational inertia an object has.
This unit brought an even clearer
understanding for me that physics is EVERYWHERE. Over Thanksgiving Break, I was
watching a show on Netflix called Revenge. In the beginning of an episode the
narrator said “Every action has an equal and opposite reaction.” Immediately I
thought of Newton’s Third Law.
Newton’s Third Law states that
every action has an equal and opposite reaction. Newton’s second law can be
explained in the formula(a=Fnet/m)
which explains that accleration is directly proportional to
force and indirectly proportional to mass. Newton’s Third Law can use this same
formula but you can write it in a different way: (F=ma).
An
example where Newton’s Third Law is put into play can be seen when a large
truck and a small car have a head on collision. The small car experiences the
greater force because even though the truck and car exert the same force, the
truck has a greater mass therefore the car will have a greater acceleration. We
know this because of Newton’s third law, which states that every action has an
equal, and opposite reaction. This means the mass and acceleration must equal each
other out so that they will have the same force. This can be described in the
formulas below:
F=ma
Car
F (10N) =ma
Truck
F (10N)=ma
Continuing
with Newton’s Third Law, we practiced action reaction pairs. If Margaret Anne
pushes Naeem, Naeem pushes Margaret Anne. The key part about these reaction
pairs is that the verb is the same (equal force) and the reaction is opposite.
Another example is if an apple falls out of a tree. If the action force on the
apple is the force of gravity on the apple, the reaction to that force would be
apple pulls on earth. Of course, there are much more complicated examples as
well. Imagine a book at rest on a table. One of the forces on the book is the
support force and another force is the force of gravity on the book. So the
action reaction pairs would be; Earth pulls apple downward and apple pulls
earth upward. Table (support force) pushes apple upward and apple pushes table
downward. So then, we moved on to an example that might help us understand more
everyday things. For example, if forces are always equal and opposite then how
does a horse pull a buggy forward?
This image is an attempt to show the different forces going
on to cause the horse to pull the buggy forward. The reason the horse pulls a
buggy is because of a few things. We know the horse exerts the same force on
the buggy that the buggy exerts on the horse because of Newton’s Third Law which
states that every action has an equal and opposite reaction. But the reason the
horse and the buggy move forward is because the horse pushes on the ground with
a greater force than the buggy pushes on the ground. A key part of this drawing
is that the pink arrows are larger than the grey arrows to show that the horse
has a greater force than the buggy. So here are the action reaction pairs; the
grey would be buggy pushes on earth forward and earth pushes on buggy backward.
The orange would be, the horse pulls buggy forward and the buggy pulls the
horse backward. Lastly, the pink would be the horse pushes on the earth forward
and the earth pushes on the horse backward.
Then
we moved on to vectors, which seemed really terrifying at first but turned out
to be a lot easier and a lot more fun than I was expecting. A key example we
used was a box on a ramp. Why does it go down the ramp? We figured out the
reasoning by drawing vectors for the image.
You begin this drawing by drawing your fweight, which is the
light blue line. You then draw the navy blue line above it and make sure it’s
the same length as the fweight. This will allow you to draw the guide, which is
the black line parallel to the ramp. From there, you draw your support force
(fsupport), which is the red line, which must be perpendicular when it
intersects the guide. Then you must draw lines that are equal in size and
parallel to the fsupport and fweight. This creates the guide to draw the vector
or the fnet, which goes diagonally through and must be parallel to the ramp.
The fnet shows the direction in which the box is going, which is downhill.
This is another example of vectors. This shows which side of
the rope will be more likely to break (the ropes are the black lines connected
to the ball or circle. I started figuring this example out the same as the
previous example; I drew the fweight and then I drew a line equal its length
right above it (these are the blue lines). The blue line that is drawn above
the fweight helps to draw the parallel lines. These green lines were drawn to
be parallel to each of the ropes starting at the tip of the blue line. The pink
lines were drawn to determine the outcome of the problem. The rope on the left
will be more likely to break because it has greater tension. We know this
because the vertical pink line is greater than the one on the right.
Then
we moved on to the universal gravitational force formula. This formula is:F=G(m1m2/d^2) I saw this equation and
immediately became discouraged. I thought this unit was going to turn into a
complicated math unit that I wouldn’t understand and wouldn’t be able to relate
it to my everyday life. However, my outcome was much different than my
expectations. One of the first questions we were asked in this unit was “Where
do you weigh more, at the ocean or on the top of Mt. Everest? Why?” My
immediate response was that my weight would not change because when you tell
someone like your doctor your weight you don’t say “Well I weigh 237 lbs. at
the ocean but 234 lbs. at the top of Mount Everest.” Anyways I was proved wrong
because I learned that I weigh more at the ocean because my gravitational pull
is a lower elevation therefore it will be stronger. The distance is key. At the
top of Mt. Everest I weight much less because I am at a much higher elevation
therefore my gravitational pull will not be as strong.The longer the distance the less force
there is. The shorter the distance the bigger the force.Also, I was reminded that although my
weight would decrease my mass would remain the same. An astronaut weighs less
in space because he or she is farther away from the earth therefore their
gravitational pull is not as strong, however their mass remains the same.
To
put this equation into use we practiced a lot of problems. One of these
problems asked us to find the gravitational force between the earth and the
sun.Presuming that G=7X10^-11
Nm^2/C^2 , the distance between the earth and the sun is about 2X10^11 and the
mass of the earth is 6X10^24kg and the sun’s mass is 2X10^30. All I had to do
was plug these numbers into the formula and cancel out the exponents to solve
for the answer which is 21X10^21N.
Learning
about the earth’s gravitational pull brought us to the concept of tides. The
force between the earth and the moon is greater than the force between the sun
and the earth because the moon is CLOSER. Therefore, the moon affects these
tides. Tides are caused by the difference in force felt by the opposite sides
of the earth. Whichever side is closer to the moon will feel the greater force.
There are two high tides and two low tides each day (4 tides per day total).
High to low tide has a time span of 6 hours and from high tide to high tide and
low tide to low tide there is a time span of twelve hours. There is not a specific
time each day at which these tides occur. It’s constantly changing because the
moon is constantly orbiting the earth. It takes about 27 days for the moon to
complete a full orbit. There is a tidal bulge that forms around the earth.
There are two tides we learned about called neap tides and spring tides. During
spring tides the moon is either a full moon or a new moon and the tides are at
its highest highs and lowest lows. Hurricane Sandy was so destructive because
it came at a full moon therefore it was a spring tide so the tides were at its
most extreme. If Hurricane Sandy had come during a neap tide or a half moon,
the damage would have been much less severe. This is because during neap tides,
the high tides aren’t as high as usual and they aren’t as low as usual. Here
are images of each to show the position of the earth, moon, and sun during each
of these tides.
This is an image of spring tides. There are two moons in
this picture two show that the moon can either be to the left or right of the earth
during spring tides. Also notice the tidal bulge is directed towards wherever
the moon is. The high tides will
be where you see the tidal bulge and the low tides will be above and below the
earth.
This is an image of neap tides. Again there are TWO moons in
this picture to show that the moon can either be directly above or below the
earth during neap tides. Also notice the tidal bulge is directed towards
wherever the moon is. The high tides
will be where you see the tidal bulge and the low tides will be to the left and
right of the earth. (High tides and low tides occur on opposite sides of the
earth.)
An
important note to keep in mind when thinking about tides is that lakes don’t
experience tides. Lakes don’t experience tides like the ocean does because the
mass of the lake is not nearly big enough to be affected by the pull of the
moon. Next,
we moved on to momentum and impulse. Momentum can be defined as inertia in
motion or the product of the mass of an object and its velocity. Momentum= mass
x velocity or Momentum=mv. To simplify this formula further, we use P to
represent momentum so the official formula used to find the momentum of an
object is P=mv. Impulse
is the change in force.Impulse=
quantity force x time interval. Impulse= Ft. We use J to represent impulse. So
the official formula is J=Ft.
Impulse changes momentum. Therefore impulse= the change in momentum. Ft=
change (mv). You can increase momentum by increasing the mass or increasing its
speed. In other words to increase (change) impulse you can either increase the
force or change the time interval. This was seen when we did the egg toss in
class. Naeem and Ethan won because they decrease the impact in which the egg
landed. They changed its momentum by increasing its time (which decreased its
force).
P=mv
P=mv
P=mv
We must also take into consideration the conservation of
momentum. This by definition states that in the absence of a new external
force, the momentum of an object or system of objects is unchanged. The formula
for this is mv(before)=mv(after). Therefore the change in P will always equal
Pfinal-Pinitial.
Change
in P= Pfinal- Pintial
Change
in P=mvfinal-mvinitial
Take airbags into consideration. Why do airbags keep us
safe? Air bags keep us safe because they slow down the force by increasing the
time. The change in momentum is always the same with the dash or the airbag. P=mv.
Change in P= Pfinal-Pinitial. If change in P is the always the same so is the
impulse whether you hit the dash or the airbag. J=Change in P. However, the
airbag increases the time of the impulse so the force on you is less. Small
force=less injury. J=F(change)t. No airbag J=F(change)t
With airbag J=f(Change)time.
Impulses
are greater when an object bounces off an object. Impulse required to bring an
object to a stop and then “throw it back again” is a greater impulse than the
impulse required to just bring an object to a stop. This also ties into the
conservation of momentum. Newton’s second law states that net force must be
applied for acceleration. If you want to change momentum you must exert
impulse. Only an impulse external to a system can change the momentum of the
system. Otherwise the change in momentum will be the same before and after. For
example, car bumpers are made of plastic and no longer made of rubber, which
was popular for awhile, because the rubber bounces therefore a greater force
would be exerted upon the car because according to Newton’s Third Law every
action must have an equal and opposite reaction whereas plastic doesn’t bounce
therefore the force exerted will be smaller. The plastic crumples which
increases time however the impulse is the same.
Ja=-Jb
Change in Pa= -Change in Pb
Change in Pa+Change in Pb=0
Conservation of momentum says that impulse causes the
momentum forces to be equal and opposite. Impulse causes the change in
momentum.
Change in P=J
J=F(change)t
Ptotal before= Ptotal after
Ma+Va+Mb+Vb(before)=(Ma+Mb) Vab (after)
Momentum is only conserved with a system. The total momentum before and after are
always the same but individually the momentums can change.
In this picture, it is high tide. The water levels are at
its highest point before shifting to low tide. Shifts from high tide to low
tide occurs every six hours, therefore there are four tides per day (two high
tides and two low tides).These
tides never occur at the same exact time each day. This is because the moon
affects these tides. Tides are caused by the difference in force felt by
opposite sides of the earth. The force between the earth and the moon is greater
than the force between the sun and the earth because the moon is much closer. The
moon takes 27 days to completely orbit around the earth. As a result the time
of day and level of tides is constantly changing. There are spring tides that
occur about two times a month. Spring tides are when the moon is directly in
line with the sun and the earth. Spring tides have the highest high tides and
the lowest low tides. The moon is full during spring tides. There are also neap tides, which occur
when the moon is directly above or below the earth. Neap tides are tides that don’t
have the highest high or the lowest low. The moon is halved during neap tides.
