This
unit was particularly interesting because the physics we learned seemed to
relate to ever day activities even more than before. There are three main topics we learned about this unit;
rotational and tangential velocity, rotational inertia, the conservation of
angular momentum, torque, center of mass/gravity, and centripetal and
centrifugal forces.
Rotational
velocity is the number of complete rotations per time unit. Tangential velocity
can also be called linear speed because it is something moving a long a
circular path. The direction of motion is tangent to the circumference.
Tangential speed depends on the distance from the axis of rotation. Take a
merry-go round for instance, the closer you are to the middle the slower you
are going whereas on the outside you feel as though you are going much faster.
This is because the people on the outside are farther from the axis of
rotation. Everyone has the same rotational speed. Their rotational speed is
dependant upon the number of spins the platform of the merry-go round has per
time unit.
Another example is a track race. If
everyone started in an exact straight line, the race would be unfair because
the people on the outside would have to have a greater speed to keep up with
the people closer to the axis of rotation who would not need to go as fast. The
runners on the outside would have a greater tangential velocity than the
runners on the inside. Each runner has his or her own rotational speed
depending on the speed in which they are going.
Have you ever seen a car with tires
much too big for its frame? Well these people most likely get speeding tickets
frequently if they are not careful. A speedometer is accustomed to a specific
size of tires, therefore when you get larger tires than the speedometer is
accustomed to the car might read 40mph but you are really going 60mph. Although
your rotational speed decreases, your tangential speed increases and you are
covering a greater distance in a smaller amount of time because your wheels are
larger.
The last example we learned a lot
about is the wheels of a train. The wheels are designed with the wider parts in
the middle rather than the outside. The wider parts are in the middle because
the wider parts will allow the wheels to turn and go straight. The smaller
parts of the wheel will want to turn and the larger parts will direct the
wheels to remain on the tracks. In this scenario the left diameter on the track
is smaller than the right therefore it will move slower and the right will move
faster causing the wheel to curve inward. If it shifts too far where the larger
diameter is on the left, it will move faster causing the train to curve in the
opposite way, it is a method of self-correction.
Moving on to rotational inertia;
Inertia is the property of an object to resist change in motion dependant upon
the mass. Rotational inertia is the property of an object to resist changes in
the spin of an object. It is dependant upon, not the mass of each object, but
where the mass is located on that object, how it is distributed. It involves the distribution of mass and
how far away it is from the axis of rotation. If an object has a small amount
of rotational inertia, it is easier to spin compared to an object with a large
amount of rotational inertia, which is very difficult to spin.
Rotational inertia explains why
runners bend their legs instead of keeping them straight. By bending their
legs, their mass is closer to the axis of rotation lowering the rotational
inertia.
This can also explain how an ice
skater spins. When the ice skater has their leg and arms spread out and
spinning, their rotational inertia is much greater because her limbs are
farther away from his/her axis of rotation, therefore the ice skater is
spinning very slowly. However, if an ice skater brings in his/her arms and
legs, her rotational inertia decreases because she is bringing her mass closer
to her axis of rotation.
The conservation of angular and
rotational momentum is basically the same concept as the conservation of
momentum. Angular momentum is made up of two key factors: rotational inertia
and rotational velocity. Angular
momentum before equals the angular momentum just as the total momentum before
equals the total momentum after.
Conservation of Angular Momentum:
Rotational inertia X Rotational
Velocity (before) = Rotational inertia X Rotational Velocity (after)
Here’s an example of the ice skater
with angular momentum;
RI X rv (before) = ri X RV (after)
In this example, the ice skater started out with a large
rotational inertia (because she had her mass far from her axis of rotation)
therefore she had a small rotational velocity. Then, she had a small rotational
inertia (because she brought in her mass closer to her axis of rotation) and
had a large rotational velocity. We know this is true because of the conservation
of angular momentum, which informs us that the momentum before will always end
up equaling the momentum after.
Torque
is what causes an object to rotate. It equals the force of an object multiplied
by its lever arm (which is the distance from an object of rotation). If an
object has a large torque, it will have a large torque. A torque is the rotational counterpart
of force. Force changes the motion of objects whereas torque changes the
rotation. Just like rotational inertia, torque involves the distance from the
axis of rotation. This distance with torque is known as the lever arm.
In
this example, the ball on the left is hollow, therefore it a smaller force than
the ball on the right who has a larger force and although the both the ball on
the left side of the seesaw and the ball on the right side of the seesaw have
equal lever arms, the ball on the right has a greater torque because it has a
larger force therefore it has a larger torque.
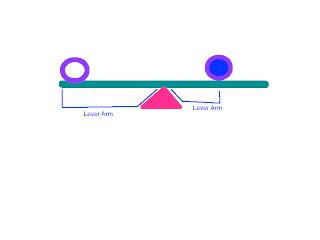However,
in this image notice that the lever arm on the left is larger than the lever on
the right. Therefore, the small force and large lever arm on the left balance
out the large force and small lever arm on the right. The lever arm on the left
was increased by simply having a greater distance from the axis of rotation.
This
is also common when dealing with bolts and wrenches. If there is a tight bolt,
you would want to have a wrench with a large lever arm because by just creating
a greater distance from the axis of rotation the force required to turn the
object will decrease and the amount of torque will be greater.
The
center of gravity is a term commonly used to express the center of mass. The
center of gravity is the average position of weight distribution. Center of
mass and center of gravity refer to the same point of an object. The center of
gravity must be above the base of support. When the center of gravity is
outside the base of support a torque happens. The center of gravity lies
directly beneath the point of suspension. The center of mass of an object may
be a point where no mass exist.
An
example where we see the center of gravity is the Leaning Tower of Pisa which
has the center of gravity lying above its base of the support therefore the
tower does no fall over. An object with a wide base and a lower center of
gravity is more stable.
A
centripetal force is a center seeking force. A centrifugal force is a center
fleeing force, however, it is a fictitious force. Think about a car going
around a turn. The friction between the tires and the road provides the
centripetal force that holds the car in a curved path. However if the friction
is not great enough, the car will skid off the road.
However,
inside this rotational system there seems to be an outward force. This outward
force is the centrifugal force. An example that might be able to explain this
more easily would be if you were a passenger of the car that was rounding the
turn. The car is turning left and you move outward to the right, technically
this was not because of a centrifugal force, it was because there wasn’t a centripetal
force to keep you in a circular motion.
This
unit was surprisingly difficult for me. The concept I struggled with the most
was torque. I was confused by the difference between torque and rotational
inertia. However, after going into conference period, I realized I needed to re
watch the torque video. In doing this, I mastered the concept and I examples in
the book involving torque.
My
problem skills throughout this unit progressively increased. At first, I
struggled with going into depth with each of the concepts presented to us. I
didn’t realize that I wasn’t going into enough depth until I began struggling
with torque. I realized I needed to be able to relate each of these concepts to
one another. So, I reviewed my notes from the previous videos and tried to find
any gaps I didn’t understand. To clarify my confusion on specific example, I
discovered that the book is actually really helpful. I think that was my key
discovery in my problem solving skills this unit (the book). My homework effort
this unit was very high and I didn’t miss an assignment and each assignment I completed
I didn’t think was just busy work, it was helpful when looking back and
studying it. Although I had a high effort in homework this unit, I need to work
on my participation in class. I am always focused in class, yet I don’t raise
my hand enough to ask questions or to answer questions. I think this could
really help me with clarifying concepts for me.
Our
podcast was a little frustrating because our group had a hard time coming up
with what to say, however, the product ended up as a really great study tool.
No comments:
Post a Comment